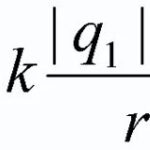什么是电位和两点之间的电位差

电势的概念是静电学和电动力学理论的重要基础之一。了解其本质是进一步研究这些物理学分支的必要条件。

什么是电势

让一个单位电荷 q 放置在由固定电荷 Q 产生的场中，该电荷 Q 受以下因素影响 库仑力 F=k*Qq/r。

此处及以下 k=((1/4)*π* ε* ε)，其中 ε_{0 —} 电常数（8.85*10^-12 F/m)，而 ε 是 介质介电常数.

贡献了 收费 在这个力的作用下，它可以移动，这个力会做一定的功。这意味着由两个电荷组成的系统的势能取决于两个电荷的大小和它们之间的距离，而这个势能的大小不取决于电荷 q 的大小。这里引入了电势的定义——它等于场的势能与电荷大小的比值：

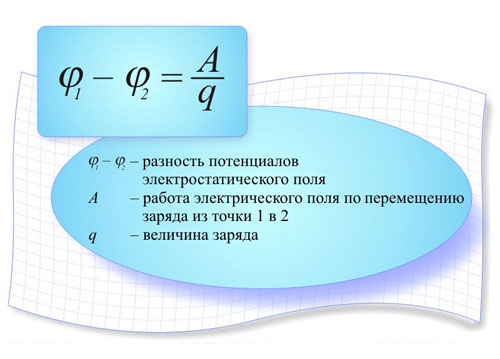
φ=W/q，

其中 W 是由电荷系统产生的场的势能，势是场的能量特征。为了使电荷 q 在电场中移动一段距离，需要花费一定的功来克服库仑力。一个点的电势等于将一个单位电荷从该点移动到无穷远所必须消耗的功。在此过程中，应注意：

• 这个功等于电荷势能的减少（A=W₂-W₁);
• 功不取决于电荷的轨迹。

在 SI 系统中，电势的单位是一伏特（在俄罗斯文学中用字母 V 表示，在外国文学中用字母 V 表示）。 1 V \u003d 1J / 1 C，即我们可以谈论1伏点的电势，如果需要1焦耳将1 C的电荷移动到无穷大。这个名字是为了纪念意大利物理学家亚历山德罗·沃尔塔，他为电气工程的发展做出了重大贡献。

为了可视化电位是什么，可以将其与两个物体的温度或在空间中不同点测量的温度进行比较。温度是物体加热的量度，电势是电荷量的量度。据说一个物体比另一个物体受热更多，也可以说一个物体带电多，另一个物体带电少。这些机构具有不同的潜力。

势的值取决于坐标系的选择，因此需要一定的水平，必须取为零。例如，在测量温度时，可以将融冰的温度作为基线。对于电位，通常将无限远点的电位视为零电平，但为了解决一些问题，例如，可以将地电位或其中一个电容器极板的电位视为零。

潜在属性

在电位的重要属性中，应注意以下几点：

• 如果该场由多个电荷产生，则特定点的电势将等于每个电荷产生的电势的代数（考虑电荷的符号）总和 φ=φ₁+φ₂+φ₃+φ₄+φ₅+…+φ_n;
• 如果与电荷的距离使得电荷本身可以被认为是点电荷，那么总势由公式 φ=k*(q₁/r₁+q₂/r₂+q₃/r₃+…+q_n/r_n)，其中 r 是与所考虑点的相应电荷 then 的距离。

如果该场由电偶极子（符号相反的两个相连的电荷）形成，那么距离偶极子距离为 r 的任何点的电势将等于 φ=k*p*cosά/r²， 在哪里：

• p 是偶极子的电臂，等于 q*l，其中 l 是电荷之间的距离；
• r 是到偶极子的距离；
• ά 是偶极臂与半径矢量 r 之间的角度。

如果该点位于偶极子的轴上，则 cosά=1 且 φ=k*p/r².

潜在差异

如果两点具有一定的电位，如果不相等，则称两点之间存在电位差。点之间发生电位差：

• 其潜力由不同符号的电荷决定；
• 一个具有任意符号电荷电位的点和一个电位为零的点；
• 具有相同符号势但绝对值不同的点。

也就是说，电位差不取决于坐标系的选择。可以用相对于零标记（例如海平面）位于不同高度的水池进行类比。

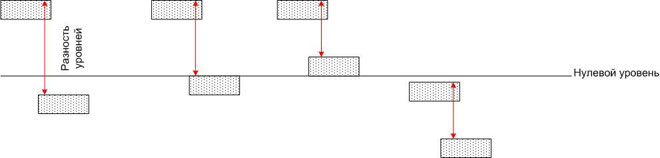
每个水池的水都有一定的势能，但是如果你用一根管子把任意两个水池连接起来，那么每个水池里都会有水流，水流的流速不仅取决于管子的大小，还取决于地球引力场中势能的差异（即高度差）。在这种情况下，势能的绝对值无关紧要。

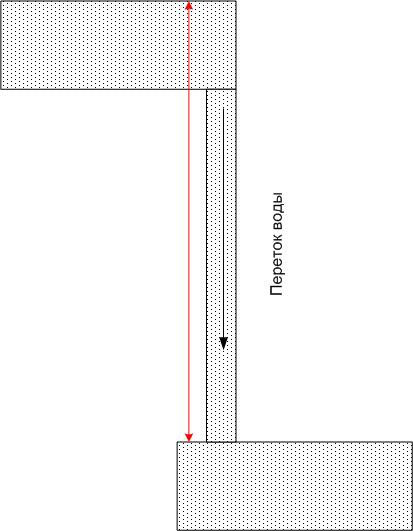
同理，如果用导体连接两个电位不同的点，它就会流动 电，不仅取决于导体的电阻，还取决于电位差（而不是它们的绝对值）。继续以水进行类比，我们可以说上层水池中的水很快就会用完，如果没有力量将水向上移动（例如泵），那么水流将很快停止。

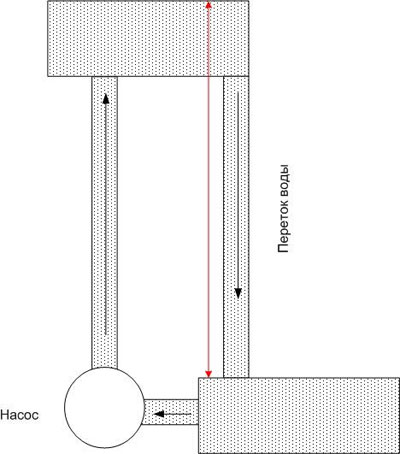
所以它在电路中 - 为了将电位差保持在一定水平，需要一种力将电荷（更准确地说，电荷载流子）转移到具有最高电位的点。这种力称为电动势，缩写为 EMF。 EMF 可以具有不同的性质——电化学、电磁等。

在实践中，重要的是电荷载流子轨迹的起点和终点之间的电位差。在这种情况下，这种差异称为电压，在 SI 中也以伏特为单位。如果将1库仑的电荷从一个点移动到另一个点时，如果场做1焦耳的功，我们可以说1伏特的电压，即1V \u003d 1J / 1C，而J / C也可以是单位潜在差异。

等电位面

如果几个点的电位相同，并且这些点形成一个面，那么这样的面称为等势面。例如，这种性质具有围绕电荷的球体，因为电场在所有方向上均等地随着距离而减小。

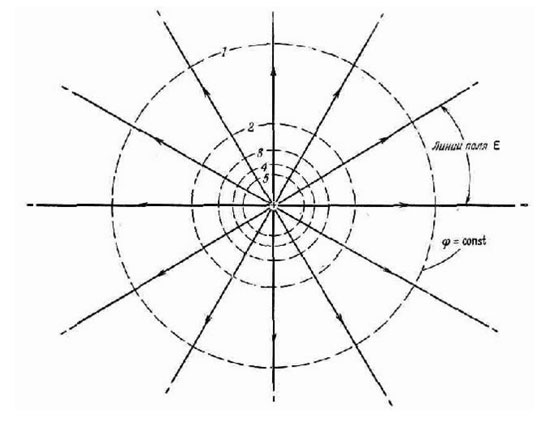
这个表面的所有点都具有相同的势能，因此当在这样的球体上移动电荷时，不会消耗任何功。多个电荷系统的等势面具有更复杂的形状，但它们有一个有趣的特性——它们从不相交。电场的力线总是垂直于在每个点处具有相同电位的表面。如果等电位面被一个平面切割，将得到一条等电位线。它具有与等势面相同的性质。例如，在实践中，放置在静电场中的导体表面上的点具有相等的电位。

处理完电位和电位差的概念后，您可以继续进一步研究电现象。但不是更早，因为不了解基本原理和概念，就不可能加深知识。

类似文章：