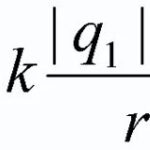洛伦兹力和左手定则。带电粒子在磁场中的运动

置于磁场中导体通过它经过电, 受安培力的影响 $F A$ , 其值可以使用以下公式计算：

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

在哪里 $我$ 和 $l$ - 电流强度和导体长度， $乙$ – 磁场感应， $\α$ - 电流强度和磁感应方向之间的夹角。为什么会这样？

洛伦兹力。带电粒子在磁场中的运动。

内容

1 什么是洛伦兹力 - 确定它何时发生，获得公式
2 使用左手定则确定洛伦兹力的方向
3 带电粒子在磁场中的运动
4 洛伦兹力在工程中的应用

什么是洛伦兹力 - 确定它何时发生，获得公式

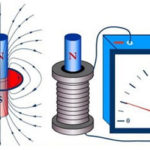
众所周知，电流是带电粒子的有序运动。还已经确定，在磁场中运动期间，这些粒子中的每一个都受到力的作用。为了产生力，粒子必须处于运动状态。

洛伦兹力是带电粒子在磁场中运动时作用于它的力。它的方向与粒子速度和磁场强度矢量所在的平面正交。洛伦兹力的合成就是安培力。知道了它，我们可以推导出洛伦兹力的公式。

粒子通过导体段所需的时间， $t = \frac {l}{v}$ ，在哪里 $l$ - 段的长度， $v$ 是粒子的速度。在此期间通过导体横截面转移的总电荷， $Q = I\cdot t$ .在这里代入前面等式的时间值，我们有

$Q = \frac {I\cdot l}{v}$ (2)

在同一时间 $F_A=F_L\cdot N$ ，在哪里 $ñ$ 是所考虑的导体中的粒子数。其中 $N = \frac {Q}{q}$ ，在哪里 $q$ 是一个粒子的电荷。将值代入公式 $问$ 由（2）式可得：

$N = \frac {I\cdot l}{v\cdot q}$

这样，

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

使用（1），前面的表达式可以写成

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

收缩和转移后，出现计算洛伦兹力的公式

$F_L = q\cdot v\cdot B\cdot sin\alpha$

鉴于公式是针对力模量编写的，因此必须编写如下：

另请阅读：如何将安培转换为瓦特，反之亦然？

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

因为 $sin\alpha = sin(180^{\circ} - \alpha)$ , 然后计算洛伦兹力模量，速度的方向无关紧要 - 在当前强度的方向或相反的方向上 - 我们可以说 $\α$ 是由粒子速度和磁感应矢量形成的角度。

以向量形式编写公式将如下所示：

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\times \vec{B}]$ 是一个叉积，其结果是一个模数等于的向量 $v\cdot B\cdot sin\alpha$ .

由式(3)可知，在电流和磁场方向垂直的情况下，洛伦兹力最大，即当 $\alpha = 90^{\circ}$ , 并在它们平行时消失 ( $\alpha = 0^{\circ}$ ).

必须记住，为了获得正确的定量答案 - 例如，在解决问题时 - 应该使用 SI 系统的单位，其中磁感应以特斯拉（1 T = 1 kg s⁻²·但⁻¹), 力 - 牛顿 (1 N = 1 kg m/s²），电流强度 - 以安培为单位，以库仑为单位充电（1 C = 1 A s），长度 - 以米为单位，速度 - 以 m / s 为单位。

使用左手定则确定洛伦兹力的方向

由于洛伦兹力在宏观物体世界中表现为安培力，因此可以使用左手定则来确定其方向。

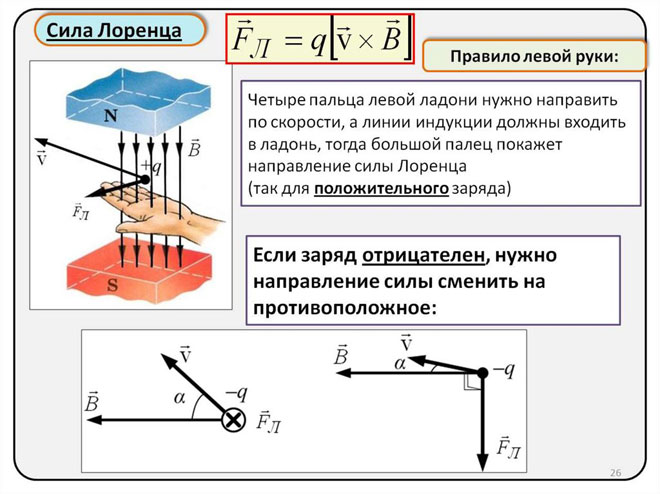
根据左手定则确定洛伦兹力的作用方向。

你需要将左手放开，使张开的手掌垂直并朝向磁场线，四指应顺着电流强度的方向伸出，然后洛伦兹力将指向拇指指向的地方，即应该弯曲。

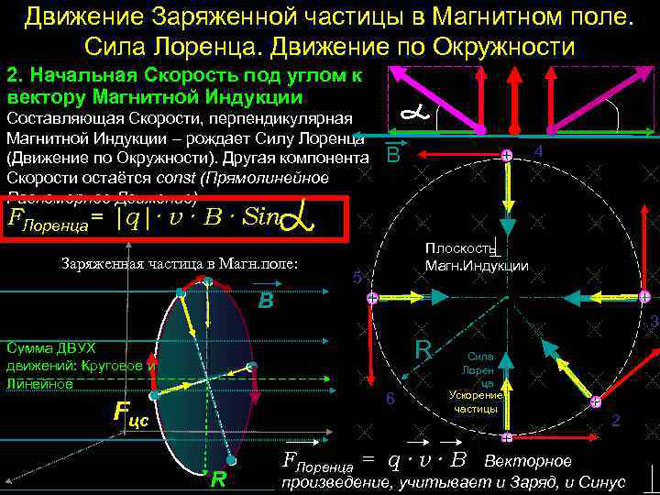
带电粒子在磁场中的运动

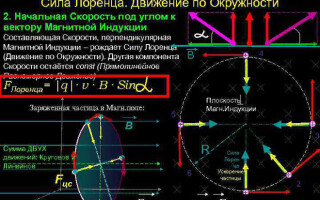
在最简单的情况下，即当磁感应和粒子速度的矢量正交时，垂直于速度矢量的洛伦兹力只能改变其方向。因此，速度的大小和能量将保持不变。这意味着洛伦兹力的作用类似于力学中的向心力，粒子做圆周运动。

另请阅读：一千瓦等于多少瓦？

根据牛顿 II 定律 ( $F = m\cdot a$ ) 我们可以确定粒子的旋转半径：

$N = \frac {m\cdot v}{q\cdot B}$ .

应该注意的是，随着粒子比电荷的变化（ $\frac {q}{m}$ ) 半径也会改变。

在这种情况下，旋转周期 T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ .它不依赖于速度，这意味着不同速度的粒子的相互位置将保持不变。

带电粒子在均匀磁场中的运动。

在更复杂的情况下，当粒子速度和磁场强度之间的角度是任意的时，它将沿着螺旋轨迹移动——由于平行于场的速度分量是平移的，并且在其影响下沿着圆移动。垂直分量。

洛伦兹力在工程中的应用

显象管

直到最近，每台电视机中的显像管都被 LCD（平面）屏幕取代，如果没有洛伦兹力，它就无法工作。为了从狭窄的电子流在屏幕上形成电视光栅，使用了偏转线圈，其中产生了线性变化的磁场。水平线圈将电子束从左向右移动并返回，人员线圈负责垂直移动，将电子束从上到下水平移动。同样的原理用于示波器 - 用于研究交流电压的设备。

质谱仪

质谱仪是一种利用带电粒子的旋转半径对其特定电荷的依赖性的设备。其工作原理如下：

带电粒子源在人为产生的电场的帮助下加快速度，被放置在真空室中，以排除空气分子的影响。粒子从源中飞出，沿着圆弧穿过，撞击照相底片，在底片上留下痕迹。根据具体的电荷，轨迹的半径会发生变化，因此影响点也会发生变化。这个半径很容易测量，知道了它，你就可以计算出粒子的质量。例如，在质谱仪的帮助下，研究了月球土壤的成分。

另请阅读：与电有关的职业有哪些

回旋加速器

周期的独立性，以及带电粒子的旋转频率与其在磁场存在下的速度的关系，被用于称为回旋加速器的设备中，旨在将粒子加速到高速。回旋加速器是两个空心金属半圆柱体 - 一个 dee (在形状上，它们中的每一个都类似于拉丁字母 D) 将直边彼此靠近放置。

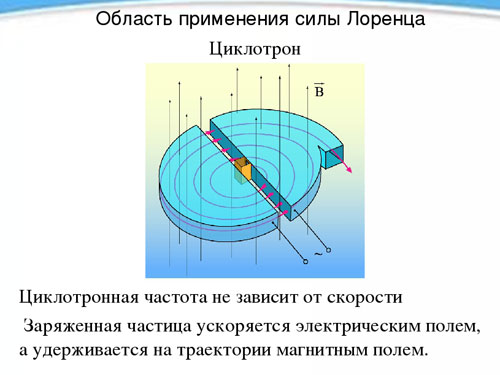
回旋加速器 - 洛伦兹力的应用。

dees被放置在一个恒定的均匀磁场中，它们之间会产生一个交变电场，其频率等于粒子的旋转频率，由磁场强度和比电荷决定。在电场的影响下，粒子在旋转期间（从一个dee到另一个dee的过渡期间）获得两次，每次加速，增加轨迹的半径，并在某个时刻获得所需的速度，通过孔飞出设备。通过这种方式，质子可以加速到 20 MeV 的能量（兆电子伏特).